EQUAÇÃO GERAL DE GRACELI.

 G ψ = E ψ =  E [G+].... ..  =

G ψ = E ψ =  E [G+ψ ω /c] =   [/ ] /  /   = ħω [Ϡ ]  [ξ ] [,ς]   ψ μ / h/c ψ(x, t)  [x  t ]..

SISTEMA GRACELI DE:

 TENSOR G+ GRACELI = SDCTIE GRACELI, DENSIDADE DE CARGA E DISTRIBUIÇÃO ELETRÔNICA, NÍVEIS DE ENERGIA, NÚMERO E ESTADO QUÂNTICO. + POTENCIAL DE SALTO QUÂNTICO RELATIVO AOS ELEMENTOS QUÍMICO COM O SEU RESPECTIVO  E ESPECÍFICO NÍVEL DE ENERGIA., POTENCIAL DE ENERGIA, POTENCIAL QUÍMICO,  SISTEMA GRACELI DO INFINITO DIMENSIONAL.

ONDE A CONFIGURAÇÃO ELETRÔNICA TAMBÉM PASSA A SER DIMENSÕES FÍSICO-QUÍMICA DE GRACELI.

A Energia de Fermi é a energia do nível ocupado mais energético em um sistema quântico fermiônico à temperatura de zero absoluto. A definição estende-se também a sistemas acima do zero absoluto, caso em que a energia de fermi corresponde à energia obtida mediante uma média das energias dos níveis quânticos com probabilidade de ocupação - devido à agitação térmica - diferentes da unidade, cada qual ponderado pela respectiva probabilidade de ocupação. Associa-se via de regra à energia de fermi a notação E_F, e a nomenclatura retrata nítida homenagem ao físico ítalo-americano Enrico Fermi.

Introdução

Contexto geral

A energia de Fermi é importante na hora de entender o comportamento de partículas fermiônicas, como por exemplo os elétrons. Os férmions são partículas de spin semi-inteiro para as quais verifica-se a validade do princípio de exclusão de Pauli - que dita que dois férmions idênticos não podem ocupar simultaneamente o mesmo estado quântico. Desta maneira, quando um sistema possui vários elétrons, estes ocuparão níveis de energia maiores a medida que os níveis inferiores estejam preenchidos.

A energia de Fermi é um conceito que tem muitas aplicações na teoria dos orbitais atômicos, no comportamento dos semicondutores e na física do estado sólido em geral.

Em física do estado sólido a superficie de Fermi é a superficie no espaço de momentos na qual a energia de excitação total se iguala à energia de Fermi. Esta superfície pode ter uma topologia não trivial. Simplificadamente se pode dizer que a superfície de Fermi divide os estados electrônicos ocupados dos que permanecem livres.

Enrico Fermi e Paul Dirac, derivaram as estatísticas de Fermi-Dirac. Estas estatísticas permitem predizer o comportamento de sistemas formados por um grande número de elétrons, especialmente em corpos sólidos.

A energia de Fermi de um gás de Fermi (ou gás de elétrons livres) não relativista tridimensional se pode relacionar com o potencial químico através da equação:

${\displaystyle \mu =\epsilon _{F}\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {kT}{\epsilon _{F}}}\right)^{2}+{\frac {\pi ^{4}}{80}}\left({\frac {kT}{\epsilon _{F}}}\right)^{4}+...\right]}$ /

G ψ = E ψ =  E [G+]....  

onde ε_F é a energia de Fermi, k é a constante de Boltzmann e T é a temperatura. Portanto, o potencial químico é aproximadamente igual a a energia de Fermi à temperaturas muito inferiores a uma energia característica denominada Temperatura de Fermi, ε_F/k. Esta temperatura característica é da ordem de 10⁵K para um metal a uma temperatura ambiente de (300 K), pelo que a energia de Fermi e o potencial químico são essencialmente equivalentes. Este é um detalhe significativo dado que o potencial químico, e não a energia de Fermi, é quem aparece nas estatísticas de Fermi-Dirac.

Contexto avançado

Principais energias em estrutura de bandas para sólidos cristalinos.

Elétrons são férmions, ou seja, são partículas regidas pela estatística de Fermi. Nesta estatística, um dado estado quântico pode ser ocupado por no máximo um e não mais que um férmion, e portanto a máxima probabilidade de ocupação de um dado estado quântico é um. Os elétrons situados dentro da amostra estão confinados por um potencial atrativo exercido pelos íons positivos da rede. Conforme mostrado pela mecânica quântica, potenciais confinantes apresentam níveis de energias discretos. No caso dos átomos isto se reflete nos tão conhecidos níveis atômicos de energia e no caso dos sólidos cristalinos, a aproximação entre os átomos leva a um agrupamento dos estados em bandas de energia. Estas bandas são vistas nas relações de dispersão para os sólidos como sendo as regiões de energia permitidas para os elétrons, separadas umas das outras por janelas de energias proibidas (ou “gaps”).

Rigorosamente falando,^[1] a energia do nível de Fermi é definida em sistemas à temperatura de zero absoluto. Nesse caso, a energia do nível de Fermi é a energia do nível mais energético ocupado, visto que nessa temperatura todos os níveis com energia menor que a energia do nível de Fermi estariam ocupados (probabilidade igual a 1) e todos os níveis com energia acima, desocupados (probabilidade de ocupação nula). Para sistemas em temperaturas não nulas, não temos mais uma transição abrupta da probabilidade de ocupação, e sim uma probabilidade dada pela distribuição de Fermi-Dirac. Considera-se então como a energia do nível de Fermi a energia obtida pela média aritmética ponderada das energias de cada estado energético afetado pela excitação térmica (estados com probabilidades de ocupação diferentes de 1 ou 0) pesadas cada qual pela respectiva probabilidade de ocupação do estado associado. O denominador desta média será obviamente o número de estados envolvidos no processo. Repare que em acordo com a estatística de Fermi, dentre os referidos estados os menos energéticos têm probabilidade de ocupação maior do que aqueles mais energéticos. Para aproximação de elétrons livres a densidade de estados cresce com a raiz quadrada da energia, resultando em uma parábola no gráfico de energia x densidade de estados. Em semicondutores e isolantes esta dependência pode ser bem mais complicada.

Outra definição equivalente implica dizer que a energia de Fermi corresponde ao potencial eletroquímico do sistema na temperatura de zero absoluto. Uma extensão a temperaturas maiores é evidente, e a energia de Fermi corresponde assim ao potencial eletroquímico do sistema na temperatura considerada. A energia de Fermi expressa, portanto, qual seria a variação da energia interna total do sólido, considerado sempre como sistema isolado e em equilíbrio termodinâmico, caso um elétron fosse dele removido. Sendo E_N^total a energia total do sistema no estado neutro, em seu equilíbrio termodinâmico, e E_N-1^total a energia total do sistema também em seu novo equilíbrio termodinâmico mas após a remoção do elétron, temos que:

E_F = E_N^total - E_N-1^{total /}

G ψ = E ψ =  E [G+]....  

Nas definições acima, o nível de referência é o nível de menor energia disponível aos N elétrons, e a remoção de um elétron provoca, então, a redução da energia do sistema. Neste referencial a energia de Fermi é, portanto, positiva, bem como o potencial eletroquímico.

Quando dois materiais diferentes são colocados em contato, a condição de equilíbrio termodinâmico exige que as suas energias de Fermi sejam iguais. Se as energias de Fermi fossem diferentes, a passagem de um elétron do sólido com maior energia de Fermi para o sólido com menor energia de Fermi resultaria em uma diminuição da energia total do sistema e o sistema composto não estaria, então, em sua configuração de equilíbrio, a de mínima energia, conforme exigido pelas leis da termodinâmica. Este fato dá origem a um fenômeno conhecido por diferença de potencial de contato que encontra diversas aplicações práticas, a saber na eletrônica de estado sólido (junção PN) e no uso do metal de sacrifício em navios.

Ilustração do conceito para compartimento monodimensional quadrado

A monodimensional compartimento quadrado infinito é um modelo para uma caixa mono dimensional. É um sitema modelo padrão em mecânica quântica para o qual a solução para uma partícula isolada é bem conhecido. Os níveis são marcados por um único número quântico n e as energias são dadas por

${\displaystyle E_{n}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n^{2}\,}$. /

G ψ = E ψ =  E [G+]....  

Suponha-se agora que em vez de uma partícula nesta caixa nós temos N partículas na caixa e que estas partículas são férmions com spin 1/2. Então somente duas partículas podem ter a mesma energia i.e. duas partículas podem ter a energia de ${\displaystyle E_{1}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}}$, //G ψ = E ψ =  E [G+]....  

ou duas partículas podem ter energia  e assim por diante. A razão que duas partículas podem ter a mesma energia é que uma partícula de spin 1/2 pode ter um spin de 1/2 (spin "acima") ou um spin de -1/2 (spin "abaixo"), conduzindo a dois estadois para cada nível de energia. Quando nós olhamos na energia total deste sistema, a configuração para as quais a energia total é a menor (o estado fundamental), é a configuração onde todos os níveis de energia acima de n=N/2 estão ocupados e todos os níveis mais altos estão vazios. A energia de Fermi é consequentemente

${\displaystyle E_{f}=E_{N/2}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}(N/2)^{2}\,}$. /

G ψ = E ψ =  E [G+]....  

O caso tridimensional

O caso tridimensional isotrópico é conhecido como a esfera de Fermi.

Deixe-nos agora considerar uma caixa cúbica tridimensional que tem um lado de comprimento L (ver compartimento quadrado infinito). Este torna-se uma muito boa aproximação para descrever elétrons em um metal.

Os estados agora são marcados po três números quânticos n_x, n_y, e n_z. As energias da partícula isolada são

${\displaystyle E_{n_{x},n_{y},n_{z}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left(n_{x}^{2}+n_{y}^{2}+n_{z}^{2}\right)\,}$ /

G ψ = E ψ =  E [G+]....  

n_x, n_y, n_z são inteiros positivos.

Existem múltiplos estados com a mesma energia, por exemplo ${\displaystyle E_{100}=E_{010}=E_{001}}$. Agora deixemos colocar-se N férmions não interativos de spin 1/2 nesta caixa. Para calcular a energia de Fermi, nós veremos no caso de que N é grande.

Se nós introduzios um vetor ${\displaystyle {\vec {n}}=\{n_{x},n_{y},n_{z}\}}$ então cada estado quântico corresponde a um ponto num "n-espaço" com energia

${\displaystyle E_{\vec {n}}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}|{\vec {n}}|^{2}\,}$. /

G ψ = E ψ =  E [G+]....  

O número de estados com energia menor que E_f é igual ao número de estados que residem em uma esfera de raio ${\displaystyle |{\vec {n}}_{f}|}$ na região do "n-espaço" onde n_x, n_y, n_z são positivos. No estado básico este número iguala o número de férmions no sistema.

${\displaystyle N=2\times {\frac {1}{8}}\times {\frac {4}{3}}\pi n_{f}^{3}\,}$

Os três férmions que ocupam os mais baixos estados de energia formam uma esfera em espaço de momento. A superfície desta esfera é a superfície de Fermi.

o fator é de dois é novamente porque são doisestados de spin, o fator de 1/8 é porque somente 1/8 da esfera repousa na região onde todos n são positivos.

Nós obtemos

${\displaystyle n_{f}=\left({\frac {3N}{\pi }}\right)^{1/3}}$ /

G ψ = E ψ =  E [G+]....  

então a energia de Fermi é dada por

${\displaystyle E_{f}={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}n_{f}^{2}}$

${\displaystyle ={\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{2/3}}$ /

G ψ = E ψ =  E [G+]....  

Tais resultados em uma relação entre a energia de Fermi e o número de partículas por volume (quando nós substituímos L² com V^2/3):

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m}}\left({\frac {3\pi ^{2}N}{V}}\right)^{2/3}\,}$

 /

G ψ = E ψ =  E [G+]....  

A energia de Fermi total de um esfera de fermi de ${\displaystyle N_{0}}$ férmions é dada por

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={3 \over 5}N_{0}E_{f}}$ /

G ψ = E ψ =  E [G+]....  

${\displaystyle E_{t}={\int _{0}}^{N_{0}}E_{f}(N)dN={\int _{0}}^{N_{0}}{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N}{\pi }}\right)^{\frac {2}{3}}dN}$ /

G ψ = E ψ =  E [G+]....  

${\displaystyle ={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}{\int _{0}}^{N_{0}}N^{\frac {2}{3}}dN={\frac {3^{\frac {2}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{2mL^{2}}}\left({\frac {3}{5}}N_{0}^{\frac {5}{3}}\right)={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$ /

G ψ = E ψ =  E [G+]....  

Energia de Fermi total:

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$

 /

G ψ = E ψ =  E [G+]....  

 

Integração por substituição:

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}={\frac {3}{5}}N_{0}\left[{\frac {\hbar ^{2}\pi ^{2}}{2mL^{2}}}\left({\frac {3N_{0}}{\pi }}\right)^{2/3}\right]={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}}{10mL^{2}}}N_{0}^{\frac {5}{3}}}$ /

G ψ = E ψ =  E [G+]....  

${\displaystyle E_{t}={\frac {3}{5}}N_{0}E_{f}}$

 /

G ψ = E ψ =  E [G+]....  

A eliminação de ${\displaystyle L}$ em favor de ${\displaystyle V}$:

${\displaystyle L^{2}=V^{\frac {2}{3}}}$

${\displaystyle E_{t}={\frac {3^{\frac {5}{3}}\pi ^{\frac {4}{3}}\hbar ^{2}N_{0}^{\frac {5}{3}}}{10mV_{0}^{\frac {2}{3}}}}}$

/  G ψ = E ψ =  E [G+]....  

Energias de Fermi típicas

Anãs brancas

Estrelas conhecidas como anãs brancas tem massa comparável a nosso Sol, mas têm um raio aproximadamente 100 vezes menor. As alta densidades implicam que os elétrons estão não mais ligados a um núcleo isolado e formam um gás de elétrons degenerado. Os números da densidade de elétrons em uma anã branca são da ordem de 10³⁶ elétrons/m³. Isto significa que sua energia de Fermi é:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{e}}}\left({\frac {3\pi ^{2}(10^{36})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 3\times 10^{5}\ \mathrm {eV} \,}$ ;

/  G ψ = E ψ =  E [G+]....

Núcleos

Outro exemplo típico é as partículas em um núcleo de um átomo. Os núcleons de um núcleo atômico pode ser tratado, assim, como um gás de Fermi e como tal, modelado.^[2]

O raio do núcleo é aproximadamente^[3]:

${\displaystyle R=\left(1.25\times 10^{-15}\mathrm {m} \right)\times A^{1/3}}$ 

/  G ψ = E ψ =  E [G+]....

onde A é o número de núcleons.

O número densidade de núcleons em um núcleo é conseqüentemente:

${\displaystyle n={\frac {A}{{\begin{matrix}{\frac {4}{3}}\end{matrix}}\pi R^{3}}}\approx 1.2\times 10^{44}\ \mathrm {m} ^{-3}}$ 

/  G ψ = E ψ =  E [G+]....

Agora, como a energia de fermi somente aplica-se a férmions de mesmo tipo, deve-se dividir esta energia por dois. Isto por causa da presença de nêutrons que não afetam a energia de Fermi dos prótons no núcleo, e vice versa.^[4][5][6]

Assim a energia de fermi de um núcleo é dada por:

${\displaystyle E_{f}={\frac {\hbar ^{2}}{2m_{p}}}\left({\frac {3\pi ^{2}(6\times 10^{43})}{1\ \mathrm {m} ^{3}}}\right)^{2/3}\approx 30\times 10^{6}\ \mathrm {eV} =30\ \mathrm {MeV} }$

/  G ψ = E ψ =  E [G+]....

O raio do núcleo admite desvios em torno do valor mencionado acima, então um típico valor para a energia de Fermi normalmente dada é 38 MeV.

Dentro da estrutura que a física estatística possibilita, segue-se que com a ajuda de conjuntos estatísticos para um número médio de ocupação ${\displaystyle \langle n_{i}\rangle }$ dos estados ${\displaystyle |i\rangle }$ com a energia ${\displaystyle E_{i}}$ da estatística de Fermi-Dirac:

${\displaystyle \langle n_{i}\rangle ={\frac {1}{e^{\frac {E_{i}-\mu }{k_{B}T}}+1}}}$ / 

/  G ψ = E ψ =  E [G+]....

Onde ${\displaystyle \mu }$ é o potencial químico, ${\displaystyle T}$ a temperatura e ${\displaystyle k_{B}}$ a constante de Boltzmann.

Estes férmions, que estão sujeitos ao princípio de exclusão de Pauli, podem estar na condição de máxima ocupação, ou seja ${\displaystyle \langle n_{i}\rangle \leq 1}$. Esta condição é que a estatística de Fermi-Dirac tratará para qualquer valor de preenchimento pleno ${\displaystyle \mu }$, porque o potencial químico de um gás ideal de Fermi não é sujeito a quaisquer restrições.

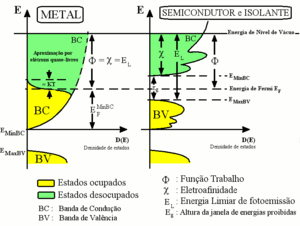
Relação fundamental em processos de fotoemissão

Equação fundamental

Conhecendo as energias anteriormente definidas estamos aptos a compreender a equação fundamental que descreve o processo de fotoemissão. Tal equação fundamenta-se no princípio da conservação da energia e considera que a energia total do sistema inicialmente em equilíbrio somada à energia do fóton incidente deve igualar-se à energia total do sistema em equilíbrio após o elétron ser ejetado, somada à energia necessária para se remover o elétron e à energia cinética deste elétron no vácuo:

${\displaystyle E_{N}^{total}+\hbar \omega =E_{N-1}^{total}+E_{cin}^{v}+\phi }$ //  G ψ = E ψ =  E [G+]....

Reagrupando os termos acima teremos:

${\displaystyle E_{B}^{v}=\hbar \omega -(E_{cin}^{v}+\phi )}$ /  G ψ = E ψ =  E [G+]....

A expressão acima corresponde à equação geral que governa o processo de fotoemissão com a referência de energia tomada necessariamente como a energia de vácuo uma vez que a energia cinética é definida no referencial da amostra e que a energia de ligação relatada também encontra-se referida à energia de vácuo. Alguns problemas práticos surgem ao se considerar um experimento real, entretanto. O primeiro refere-se ao fato que a energia de vácuo acima citada corresponde à energia de vácuo da amostra e não à energia de vácuo do dispositivo realmente responsável por medir a energia cinética dos elétrons, o analisador de elétrons. Isto se deve ao fato de que as funções trabalho do analisador e da amostra não são necessariamente iguais, e, considerando-se que ambos encontram-se eletricamente conectados, uma diferença de potencial de contato existe entre o analisador e a amostra.

A existência deste potencial de contato traz algumas implicações quanto à medida da energia cinética no analisador uma vez que a mesma implica a existência de um campo elétrico na região em vácuo compreendida entre a superfície da amostra e do analisador. Um elétron que, em relação ao nível de vácuo da amostra, possua uma energia cinética E_cin, seria percebido pelo analisador (em relação ao seu próprio nível de vácuo, portanto), como possuindo uma energia cinética dada por E_cin.medida = E_cin - e ${\displaystyle \theta }$, onde -e é a carga do elétron e ${\displaystyle \theta }$ a diferença de potencial de contato entre a amostra e o analisador (e ${\displaystyle \theta }$ = ${\displaystyle \Phi }$ _amostra - ${\displaystyle \Phi }$_analisador). O termo -e${\displaystyle \theta }$ referese à energia ganha pelo elétron ao se mover da amostra até o analisador, estando a amostra em um potencial ${\displaystyle \theta }$ abaixo do potencial do analisador. A existência da diferença de potencial de contato não seria problema caso esta fosse constante, mas quando se considera que amostras diferentes em análise possuem, cada qual, uma função trabalho diferente, na maioria das vezes previamente desconhecida, um problema real existe.

O problema atrelado ao potencial de contato reside na escolha do referencial de energia e para solucioná-lo basta portanto redefinir a energia de referência para um nível de energia comum tanto à amostra como ao analisador. Este nível de referência é evidente: a energia de Fermi.

Considerando que a diferença entre o nível de vácuo da amostra e a energia de fermi da mesma é a sua função trabalho ${\displaystyle \phi }$, a energia cinética E_CIN^F medida agora em relação ao nível de Fermi pode ser escrita como:

${\displaystyle E_{cin}^{F}=E_{cin}^{v}+\phi }$ //  G ψ = E ψ =  E [G+]....

A equação fundamental em processos de fotoemissão torna-se então:

${\displaystyle E_{cin}^{F}=\hbar \omega -E_{B}^{F}}$ //  G ψ = E ψ =  E [G+]....

Nestas equações, tanto a energia de ligação E_B^F quanto a energia cinética E_cin^F referem-se agora à energia de Fermi, e usualmente costuma-se suprimir o "^F" nesta expressão. O termo energia cinética neste caso foge, é claro, dos rigores de sua definição clássica e as energias cinéticas e de ligação E_cin e E_B usualmente encontradas nas literatura encontram-se geralmente referidas à energia de fermi. Entretanto não são poucos os em que as mesmas encontram-se referidas ao nível de vácuo de forma que alguma atenção quanto a este ponto é sempre requerida ao se consultar as tais informações na literatura.

Espectros XPS são caracterizados por uma coletânea de pontos que apresentam flutuações características, o que implica, como já citado, em uma dispersão dos pontos experimentais ao redor dos valores ideais. A extração de informações dos espectros XPS exige em uma segunda etapa, mediante o uso de programa de processamento adequado a tal fim,^[4] o tratamento e o ajuste estatístico de uma função analítica sobre os dados de cada um dos picos de interesse do espectro, dos quais resultam informações confiáveis e relevantes sobre os valores das áreas, posições e larguras dos picos de interesse. A partir destes resultados é que informações física relevantes serão inferidas.

O primeiro procedimento na análise de um pico consiste na remoção dos “elétrons de fundo”, da base na qual este se assenta. O processo mais simples para a remoção dos elétrons de fundo consiste na extração de uma base linear sob o pico no espectro original, sendo aplicável sempre que a correta identificação das posições de pontos base do pico é possível. Na maioria dos casos que envolvem semicondutores, este é o caso.

O ajuste de uma função analítica pode ser feito empiricamente ou procurando-se razões experimentais e teóricas para escolher-se a função para o ajuste, e neste caso geralmente funções gaussianas, lorentzianas, ou em certos casos uma convolução das duas prestam-se bem ao serviço de ajuste aos dados experimentais. Em sua quase totalidade os ajustes destas funções a um mesmo pico fornecem resultados semelhantes para área, posição e largura de cada pico considerado, diferindo os resultados entre os ajustes por valores menores do que as incertezas nos resultados obtidos. Na figura vemos o ajuste do pico Ga3d para um espectro obtido de uma amostra de arseneto de gálio onde depositou-se uma pequena quantidade de césio na superfície. O ajuste é feito mediante uma função gaussiana, e o ajuste por lorentziana fornece resultados bem semelhantes.

$${\displaystyle A=A_{0}+{\frac {A_{1}}{w{\sqrt {\frac {\pi }{2}}}}}e^{-2({\frac {(x-x_{c})}{w}})^{2}}}$$

 //  G ψ = E ψ =  E [G+]....

uma função gaussiana típica usada na análise de espectros XPS: os parâmetros A₀, A₁, X_c e W são ajustados pelo programa de análise de forma que a curva ajuste-se da melhor forma possível aos dados experimentais.

Em metais a remoção de uma base linear pode não mostrar-se adequada devido a uma considerável elevação do patamar de elétrons secundários no lado do pico correspondente a menores energias cinéticas, sendo exemplo deste caso o pico Fe3p em espectros de Ferro (figura abaixo, espectro para 150A de Fe). Basicamente as estruturas são simétricas para materiais isolantes e semicondutores, mas não para metais, e um tratamento diferenciado para a remoção dos elétrons secundários faz-se então necessário. Nesse último caso uma função do tipo Doniach-Sunijic ou uma aproximação desta presta-se bem melhor à correta remoção da base formada pelos elétrons secundários e o uso de uma base linear é desencorajado.